CID termina no 7º lugar

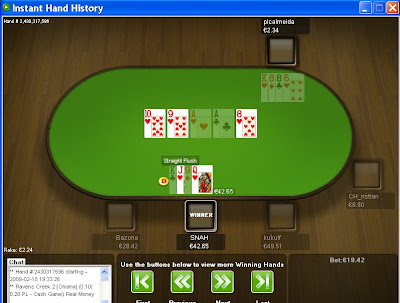
CID abre com raise all-in de 80.000 e Miguel Diniz (quem?) é o único a fazer call com A8. Já não há respeito !!!

CID exibe uns poderosos 7 6 off.

A board não ajuda o nosso Pro com 5 A K 3 K, que assim se fica por um honroso 7º lugar e mete ao bolso quase 5K

CONGRATS CID

VAMOSSSSSSSSSSSS - CID NA FT DO BETFAIR POKER OPEN

Depois de eliminar o amigo Deninja Senior, Cid Team BBF Pro entra na FT do torneio que decorre no Casino Estoril

COMPOSIÇÃO FINAL TABLE

Posição 2: Pasi Herranen 301.000 fichas
Posição 3: Jesus Ibañez 172.000 fichas
Posição 4: Miguel Neves 353.000 fichas
Posição 5: Alcídio Ferreira 465.000 fichas
Posição 6: Panu Miettinen 491.000 fichas
Posição 7: Henrique Pinho 301.000 fichas
Posição 8: Ricardo Campos 678.000 fichas
Posição 9: Diogo Silva 250.000 fichas
Posição 10: Miguel Diniz 620.000 fichas

TABELA DE PRÉMIOS
1 €31.460 -
2 €21.780 -
3 €12.100 -
4 €8.470 -
5 €7.260 -
6 €6.050 -
7 €4.840 -
8 €3.630 -
9 €3.025 -
10 €1.815 -

Doutor EZGAM...em TILT? Que se passa Bikas?

"* O Team Invitational é um torneio de equipas, apenas por convite, em que todo o prizepool será entregue às associações de solidariedade social Acreditar e Abraço.

"Por enquanto vai para estas associações da praxe...
Brevemente o guito irá para a "Entesados.com, comidos pelo Rake".

retirado de: http://noticias.pokerpt.com/49-bppt/3327-betfair-poker-open-estoril-tudo-a-postos-para-o-arranque-do-evento.html#comentarios (#18)

EPEC? O que é?

O que é a Everest Poker European Cup (EPEC)?
Vamos dar €100,000 num Freeroll aberto a jogadores Europeus de poker amadores durante a Final EPEC Ao Vivo na paradisíaca Sardenha.
Queremos que se junte a nós nesta experiência incrível. Os vencedores dos satélites de qualificação para a Final EPEC Ao vivo irão viajar até à Sardenha e competir neste excitante evento de dois dias no magnifico Chia Laguna Resort.
Os qualificados EPEC vão receber um pacote de prémios de €1.100 que lhes garante um lugar na Final da Everest Poker European Cup. O pacote de prémios de €1.100 inclui o buy-in de €500 no torneio, três noites num hotel no valor de €300 e €300 (US $450) adicionais, para despesas de viagem.

Como diria a Ferreira.."Any 2 Babydoll"...Epec - o sonho!

Vamoosssssssssss!

PETIÇÃO - AJUDEM O CHEF A COMPRAR UM iPOD

Pessoal,
Venho lançar uma Petição para que me ajudem a adquirir um iPod.
Eu sei que vocês sabem que eu já tive um, mas compreendam que o tive de deixar junto da senhora da fotografia que estava cheia de frio e totalmente descoberta (apesar de estar nas Bahamas e do ar de felicidade da mesma ao olhar para a minha objectiva grande angular quando tirei a fotografia).

Qubrei o enguiço da terrível "Bahamas"!

A partir de agora A10 é sempre a esgalhar...ao flop full é house e no river o maravilhoso four of a kind!!! lol

Yeahhhhhh!
BBF rulezzzzzzzzz!

Abracos

Bom resultado na fulltilt...Rusty Wallace strikes back

Muito forte em Omaha!!!

PokerStars Tournament #142279734, Pot Limit Omaha
Buy-In: $30.00/$3.00
72 players
Total Prize Pool: $2160.00
Tournament started 2009/02/27 3:30:00 GMT [2009/02/26 22:30:00 ET]


Dear gus_allen,

You finished the tournament in 1st place. A $595.08 award has been credited to your Real Money account.

You earned 210.50 tournament leader points in this tournament. For information about our tournament leader board, see our web site at http://www.pokerstars.com/poker/tournaments/leader-board/


Congratulations!

Thank you for participating.

3 caves em 3 mãos

OMG...RUSTY WALLACE STRIKES AGAIN!!!

Caro(a) OH_LINA,

Terminou o torneio em 1º lugar. Foi creditado na sua conta um prémio de $198,36.

Ganhou 181,81 pontos de líder neste torneio. Para informações sobre a nossa Tabela de Líderes de Torneio, visite a nossa página http://www.pokerstars.pt/poker/tournaments/leader-board/

Quando o Azar bate à Porta...Nada a fazer!!! GG me!!

José Vilela Dias tem um estômago de aço e não enjoa na montanha russa. O "zaratara" sobreviveu ao sobe e desce final da etapa da Liga PokerPT.com disputada na Mansion Poker e levou os $68,40 destinados ao vencedor.

Quando os 64 jogadores que acorreram à Mansion Poker ficaram reduzidos a apenas três, as stacks pareciam autênticas montanhas russas. Ora sobes tu, ora desço eu e ninguém conseguia apontar um favorito. Até que José Vilela Dias ficou Head's Up com "OHLINA" e este não aguentou a descida vertiginosa... E um no river acabaria por consagrar "zaratara" como o "rei da montanha russa".

Para "OHLINA", a "adrenalina" rendeu $45,60 pelo 2.º lugar, num torneio em que os 64 jogadores e os $100 adicionados permitiu distribuir um prize pool de $228 pelos 10 primeiros classificados.

Mais uma boa prestação...faltou sorte em momento crucial!!

PokerStars Torneio #137802075, No Limit Hold'em
Buy-In: $10.00/$1.00
2367 jogadores
Pacote de Prémios Total: $86270.00
Torneio começou às 2009/02/02 21:00:00 GMT [2009/02/02 16:00:00 ET]

Caro OH_LINA,

Você terminou o torneio em 175º lugar.
Um prêmio de $103.52 foi creditado em sua conta Dinheiro Real .

com este torneio você ganhou 73.95 pontos para a Tabela de Líderes de Torneios.
Para mais informações sobre a Tabela de Líderes de Torneios, visite nosso website no endereço
http://www.pokerstars.com/pt/poker/tournaments/leader-board/


Parabéns!
Agradecemos a sua participação.

Honestidade e Humildade acima de tudo!

O regresso das Bahamas foi uma desgraça a bater todos os records ao perder 2 dos 3 voos do itenerário escolhido...



Em Londres tive que esperar 8h pelo voo seguinte da TAP p/ o Porto... pelo que p/ além de ter feito mtas compras nos duty free shops pensei tb mto o quanto ridículo é perder tantas horas em escalas desnecessárias só por causa de poupar 1000 ou 1500 € nos bilhetes de avião qdo a minha win rate é superior a $1000/h.

*retirado de :http://lostlucky.blogspot.com/




Ou seja:

1000/h x 6 horas (caso jogue 6 horas/ representa uma m'edia de 6000$ dia)

$6000/dia x 6 dias semana - (representa $36000/semana)

36000$ x 4 semanas (representa $144000/mes)



Such a PERFORMANCE! ...assim percebo - o quanto ridículo é perder tantas horas em escalas desnecessárias! lololol
Grande LOST!

OMG..HE DID IT AGAIN...RUSTY WALLACE ON FIRE!

PokerStars Torneio #137239910, No Limit Hold'em
Buy-In: $8.00/$0.80
90 jogadores
Pacote de Prémios Total: $720.00
Torneio começou às 2009/01/29 21:06:30 GMT [2009/01/29 16:06:30 ET]

Caro OH_LINA,

Você terminou o torneio em 2º lugar.
Um prêmio de $133.20 foi creditado em sua conta Dinheiro Real .

com este torneio você ganhou 128.56 pontos para a Tabela de Líderes de Torneios.
Para mais informações sobre a Tabela de Líderes de Torneios, visite nosso website no endereço
http://www.pokerstars.com/pt/poker/tournaments/leader-board/

Mais algumas migalhas...valeu pelo resultado!!!

PokerStars Torneio #137036725, No Limit Hold'em
Buy-In: $8.00/$0.80
90 jogadores
Pacote de Prémios Total: $720.00
Torneio começou às 2009/01/28 21:45:00 GMT [2009/01/28 16:45:00 ET]

Caro OH_LINA,

Você terminou o torneio em 1º lugar.
Um prêmio de $198.36 foi creditado em sua conta Dinheiro Real .

com este torneio você ganhou 181.81 pontos para a Tabela de Líderes de Torneios.
Para mais informações sobre a Tabela de Líderes de Torneios, visite nosso website no endereço
http://www.pokerstars.com/pt/poker/tournaments/leader-board/

EPT Deauville S5: Entrevista con Ricardo Sousa

FABULOSO

EPT Deauville S5: Entrevista con Ricardo Sousa

"El jugador portugués, Ricardo Sousa, nos cuenta comova su primer día de torneo en Deauville."

IMPERDÍVEL em: http://www.pokerstars.tv/movies/504/ept-deauville-s5-entrevista-con-ricardo-sousa.html

Nota: Toda a entrevista é dada em espanhuel da galiza...Fabuloso!

Baseado neste sistema desenvolvi o Omaha calculator

Quem quiser esta poderosa e util ferramenta em exel, desenvolvida por ZÉ_OH_LINA é só pedirem por post que eu envio-vos para o email!

E tb o Omaha H/L...

HUTCHISON POINT COUNT SYSTEM FOR OMAHA HIGH-LOW POKER
The following is slightly modified from an article of mine that appeared in the December, 1997 issue of the Canadian Poker Monthly. I want to acknowledge with appreciation the contributions of Nolan Dalla, Dave Scharf, and others to this effort to quantify starting hands in Omaha Hi-Lo Poker (Eight or Better).
ASSUMPTIONS: A ten-handed game at the lower levels with a mix of good and poor players.


OBJECTIVE: To identify those hands that have at least a 50% above chance expectation of winning. That is, while any random hand should win about 10% of the pots in a ten-handed game, the hands identified as "playable" by this system have at least a 15% probability of winning.


METHOD: In any split pot game the best hands are those that have a chance to win both high and low. Most of the hands without this potential should be discarded. However, there are a few hands that are profitable even though they have no potential to win low.


The first step in evaluating your hand is to see if it is one of these HIGH-ONLY hands. To qualify, all four of your cards must be Ten or above AND include (1) two pair, or (2) a pair and two suited cards, or (3) two double suits. Eliminate any high hand containing three of the same rank. If your hand does not qualify as a HIGH hand, then...


The next step is to see if your hand can be played as a LOW or TWO-WAY hand. This determination is made by adding the number of points obtained in these four simple steps:


FIRST, look at your two lowest cards and award points as follows:

A-2 equals 20 pts. A-3 equals 17 pts. A-4 equals 13 pts.

A-5 equals 10 pts. 2-3 equals 15 pts. 2-4 equals 12 pts.

3-4 equals 11 pts. 4-5 equals 8 pts. Anything else = no pts.



SECOND, look at your two remaining cards ("kickers") and award points as follows:

3 equals 9 pts. 4 equals 6 pts. 5 equals 4 pts.

Jack, Queen, or King equals 2 pts. 6 or Ten equals 1 point

Do not award any "kicker" pts. for a card that duplicates a card used in step one and if
the kicker is paired it is counted only once under this step.



THIRD, if you have any pairs, add points as follows:

Aces equal 8 pts. Kings equal 6 pts. Queens equal 5 pts. Jacks equal 2 pts. Tens equal one point Fours equal one point Threes equal one point Deuces equal 3 pts.

Deduct half of the points awarded under this step if you have three cards of the same rank.


FOURTH, if you hold two suited cards and the highest of them is

an Ace, add 4 pts. a King, add 3 pts. a Queen or Jack, add 2 pts. an 8, 9, or Ten, one pt.

Deduct half of the points awarded under this step if your hand contains three cards of the same suit and award no points if all of the cards are of the same suit.


EACH HAND WILL EARN A TOTAL FROM 0 TO 45 POINTS. PLAY THOSE HANDS WITH 20 POINTS OR MORE AND CONSIDER RAISING WITH 30 POINTS OR MORE.

.

EXAMPLES FOR CLARIFICATION


You are dealt AS, 3S, 5H, KD. Since not all four cards are above Ten, the hand is evaluated as a low or two-way hand by following the four steps outlined above. Step one awards 17 pts. for the A-3, step two grants six pts. for the 5 and K "kickers," step three does not apply, and step four gives four pts. for the two suited cards (spades) headed by the Ace. The total equals 27 pts. making this a playable hand.

You are dealt AS, AC, 2S,3C. The hand does not qualify for high. Step one awards 20 pts. for the A-2, step two gives nine pts. for the 3 "kicker," step three grants eight pts. for the pair of Aces, and step four means that each double-suited combination headed by an Ace is worth four pts. each or a total of eight pts. for the two combinations. The grand total for this hand is 45 points. Incidentally, this is the most powerful hand in high-low Omaha.

You are dealt AS, TS, AC, QD. This hand qualifies for high because it satisfies the condition that 1) all four cards are Ten or above, and 2) two of the cards are paired and two are of the same suit.

You are dealt AS, TS, KD, QD. This hand qualifies for high because 1) all four cards are Ten or above, and 2) it contains two double suits.


NOTES

A very high correlation (but not a one-to-one correspondence) exists between a hand's point count and its winning percentage. Thus, a hand that earns 25 pts. is quite likely to have a higher win percentage than a hand with 24 pts.and it is almost certain to have a higher percentage than a hand with 23 or fewer pts.

It should be noted that initial card selection, while crucial to success, is not the only skill necessary to maximize Omaha profits. These other skills, however, do not lend themselves to easy quantification and are beyond the scope of this simple mathematical approach. Recall, too, the basic assumption that this system is being used at the lower limits. I hope that these limitations will not detract from the main purpose of this approach which is to provide a simple aid to the beginner.

This system has been devised by Edward Hutchison who invites your comments and opinions.

Para quem quer levar o Omaha mais a sério!!!

HUTCHISON OMAHA POINT SYSTEM
The purpose of this system is to provide a simple means of evaluating starting hands in Omaha poker. It was developed in several steps:

First, Mike Caro's Poker Probe software was used to determine the win percentage for various four card combinations when played against nine opponents. This was accomplished via a Monte-Carlo type simulation with a minimum of 50,000 hands being dealt for each starting hand. The assumption made in this type of simulation is that each hand is played to the finish. This is, of course, an unreasonable expectation, but , in the absence of detailed knowledge of each player's starting requirements, method of play, etc., it is the best means of approximating a hand's strength and earning potential.

Secondly, a number of components were examined in an effort to determine their relative contribution to the value of each starting hand. Eventually, it was decided that the primary determinants of good Omaha starting hands related to the rank of the cards and whether or not they were paired, suited, or connected.

Finally, a type of regression analysis was conducted to try and determine the relative weighting of each of these factors. The system that follows is the result of quantifying the contribution made by each of these various components.

Once the calculations are made, the resultant point total, WHEN DIVIDED BY TWO, is an approximation of the actual win percentage for a particular hand--when played to the finish against nine opponents. The correlation between point totals and win percentages, while not representing a one-to-one correspondence is, nevertheless, quite high. In fact, in about 70% of the cases the actual win percentage will be within just one point of the total points awarded by this system. This means that if the system indicates that a given hand earns, say, 40 points, you can be quite confident that the actual win percentage for this hand is between 19 and 21 points. It is very likely to win more often than a hand with 38 points and almost certain to outperform a hand with 36 points.


STEPS IN CALCULATING POINT TOTALS


FIRST, to evaluate the contribution made by suited cards, look to see if your hand contains two or more cards of the same suit. If it does, award points based upon the rank of the highest card. Repeat the procedure if your hand is double suited.

If the highest card is an ACE award 8 points
If the highest card is a KING award 6 points
If the highest card is a QUEEN award 5 points
If the highest card is a JACK award 4 points
If the highest card is a TEN or a NINE award 3 points
If the highest card is an EIGHT award 2 points
If the highest card is SEVEN or below award 1 point.

If your hand contains more than two cards of the same suit, deduct 2 points.


SECOND, to factor in the advantage of having pairs,

If you have a pair of ACES award 18 points
If you have a pair of KINGS award 16 points
If you have a pair of QUEENS award 14 points
If you have a pair of JACKS award 13 points
If you have a pair of TENS award 12 points
If you have a pair of NINES award 10 points
If you have a pair of EIGHTS award 8 points
If you have a pair of SEVENS or below award 7 points

Award no points to any hand that contains three of the same rank.


THIRD, when your hand contains cards capable of completing a straight it becomes more valuable. Therefore, If your cards contain no more than a three card gap, add the following points:

For FOUR cards, add 25 points

For THREE cards, add 18 points

For TWO cards, add 8 points

From these totals, subtract two points for each gap, up to a maximum of six points.

To account for the special case represented by ACES, deduct four points from the above totals when an Ace is used. This is necessary because an Ace can make fewer straights. However, when your hand contains small cards that can be used with an Ace to make a straight, the hand's value increases. Therefore, when your hand contains an Ace and another wheel card, add 6 points. Add 12 points for an Ace and two wheel cards.



FINALLY, a determination must be made as to which hands qualify as playable. This becomes a function of how many points one decides are necessary before entering a hand. My suggestion would be to only play hands that earn 28 points or more. It can be argued that, ignoring the rake, any hand with more than a 10 percent win rate (i.e., those with 20 points or more) is potentially profitable in the long run. Still, I have the prejudice that most players, and especially those who are relatively inexperienced, would be better advised to forsake marginal hands and to focus on those that earn 28 points or more. Recalling that a random hand will win about 10% of the time in a ten-handed game, it can be seen that playing only premium combinations of 28 points or more insures that you will always have a hand that is 40% better than a random hand. The total required to raise or to call someone's raise must also be determined subjectively. I feel that 32 points is the appropriate level, so, in summary,

YOU SHOULD CALL WITH 28 POINTS OR MORE AND CONSIDER RAISING WITH 32 POINTS OR MORE



SOME EXAMPLES FOR CLARIFICATION

The hand that has the highest win percentage in Omaha contains two ACES and two KINGS and is double suited. A hand containing the AS, KS, AH, and KH would earn 54 points under this system--calculated as follows: under step one above, the two double suits headed by the two aces earn 8 points each for a total of 16 points; step two awards 18 points for the pair of aces and 16 points for the pair of kings, or a total of 34 more points; under step three, the ace-king combination earns 4 points for its straight potential. (NOTE: The two consecutive cards earn 8 points but a deduction of 4 points is made because one of the cards is an Ace.) The resultant total of 54 points, when divided by two, closely parallels the actual win percentage for the hand which is about 26.65.

Assume you have the 9S, 8S, 9D, and 8D. Step one awards a total of 6 points for the two double suits headed by nines. Under step two, the pair of nines earns 10 points and the pair of eights earns 8 points. The last step awards 8 points for the 9-8 combination. The total of 32 points, when divided by two, is the same as this hand's actual win rate of 16 per cent.

With the QS, QD,9H, and 9C, no points are earned under step one as there are no suited cards. Step two gives 14 points for the pair of queens and 10 points for the pair of eights. Step three awards 8 points for the Q-9 combination but then calls for a deduction of 4 points because of the two card gap that exists between the two cards. The final total is 28 points and, when divided by two, it again closely reflects the actual win percentage for this hand which is 14.5%.

An example of a hand that tends to be somewhat over-rated by novice players is AS, KD, QH, and TS. Under step one the hand receives 8 points for the suited ace and ten. Step two is disregarded as the hand does not contain any pairs. Step three awards 23 points for the straight potential of the four connected cards. The final total is only 31 points, making this a marginally playable hand. It actually wins about 16.2%.

Finally, consider AS, 3S, KD, 4D. Step one awards 14 points, step two awards none, and step three grants 12 points for the A-3-4 combination and 4 points for the A-K combination. This total of 30 points corresponds with the actual win rate of 15%.


NOTES

To state the obvious: many skills other than initial card selection are essential to maximizing your profits when playing Omaha. Unfortunately, these other skills do not lend themselves to easy quantification, and are thus beyond the scope of this simple mathematical approach. I do hope, though, that this system will be of help to the novice player in making the important decision about which starting hands are worthwhile.